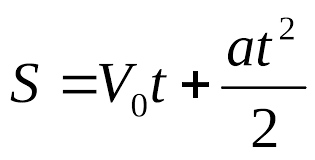"Площадь времени", что это такое?

 В школе мне старались нагружать только одно из полушарий - левое, отвечающее за логику. И всё вроде бы было правильно, когда надо решать правильные задачки и получать правильные ответы. А если не надо?

Вот сейчас не надо.

Попробую позадавать заумные вопросы из правого полушария и попробовать отвечать на них просто удовольствия для.

Известно, что в уравнении равноускоренного движения 

присутствует квадрат времени.

Меня всегда волновал вопрос.

Раз квадрат - значит площадь.

Раз площадь - значит у объекта как минимум два измерения.

Так получается что 

при вычислении равноускоренного движения у времени "открывается второе измерение", 

или что?

Попробую ответить.

Вообще говоря, для того чтобы оценить движение на ускоренность, по-моему разумению, время нужно замерить как минимум три раза. 

Первый и второй замер времени дадут информацию о первоначальной средней скорости за час. А третий замер времени даст возможность оценить не только среднюю скорость за второй час, но и ИЗМЕНЕНИЕ СРЕДНЕЙ СКОРОСТИ, если таковое имеет место.

Для того чтобы оценить является ли движение равноускоренным, нужно провести ещё одно предварительное измерение, скажем за час до того как (смотрим на картинку) велосипедист набрал скорость 10км\ч. Сравнив два ПРИРАЩЕНИЯ СКОРОСТИ, можно предположить, что если оно оказалось неизменным, то движение было равноускоренное и ускорение равно 5км\час за час. 

Если бы за каждый из отрезков времени (1 час) велосипедист проходил одно и то же расстояние, то ускорение такого движения равнялось бы нулю. (Помимо времени мы были обязаны измерять и пройденное велосипедистом расстояние, мной это как бы подразумевается.)

График равномерного движения на координатной плоскости V(t) выглядит вот так.

Также можно рассматривать тип движения велосипедиста до начала первого измерения.

Ведь ТОГДА МЫ ЕЩЕ НЕ МОГЛИ СКАЗАТЬ - ЯВЛЯЕТСЯ ЛИ ЕГО ДВИЖЕНИЕ УСКОРЕННЫМ.

Это очень важно!

И наконец вот так (смотрим на картинку выше) мы можем нарисовать график равноускоренного движения велосипедиста, ОБЛАДАЮЩЕГО на момент начала измерений НАЧАЛЬНОЙ СКОРОСТЬЮ!

Если смотреть на последнюю картинку, то за первую единицу времени (клетку по оси t) тело прошло 8 единиц длины (клеток по оси V). В этом и состоит смысл обладания начальной скоростью, а некий треугольный зелёный аппендикс сверху говорит о том компоненте, который внесло ускорение за эту единицу времени. За вторую единицу времени (вторая клетка по оси t) те же восемь и аппендикс побольше (два раза по ускорению).

За третью - восемь и три ускорения...

...По истечении пяти единиц времени вклад ускорения в общую скорость подрос до одной клетки. Можно сказать, что начальная скорость начиная с 6-й единицы времени равна девяти клеткам. Поскольку движение равноускоренно, то, по истечении десяти единиц времени, ускорение внесло вклад доведённый до двух клеток.

Ещё раз хочу проговорить, что в каждый последующий момент времени ситуация с прохождением за один временной цикл повторяется практически полностью. Скорость в каждый новый временной цикл (клетка по оси t) меняется только на величину ускорения. То есть тело проходит за один временной цикл на Дельта Икс (изменение координаты) больше. Весь вопрос в том как определять прирост этой "дельты", если она постоянно растёт. Можно усреднять, за период, а можно уменьшать период до неразумномелких, непредставимо мелких величин времени, которые официально называют бесконечномалыми величинами времени.

Для равноускоренного движения всё просто. 

Мы просто УСРЕДНЯЕМ!

Из геометрии хорошо виден красивишный зелёненький прямоугольненький треугольник ПЛОЩАДЬ КОТОРОГО (смотрим на график) и будет являться приращением координаты за счёт ускорения за десять временных циклов.

Стоп стоп!!! Говорю я тут себе, вот оно то место, когда мы начинаем перемножать одно время на другое, а значит вырастает вторая временная координата, то есть второе временное измерение! Как это я не заметил откуда и как это произошло?

Так что же я перемножаю и зачем?

Я перемножаю разы которые повторился временной цикл (неизменный, синхронизированный, но один и тот же). И тело проходило за каждый из этих временных циклов то же самое расстояние, что в предыдущем плюс приращение за счёт равноускоренности. То есть "циклы" были и у пространства. Скорость - это вообще нечто общее ("км в час"). Количество РАЗ скорости за один РАЗ времени. 

Что же меняется при замере времени в первый раз и во второй?

Усреднение!
ОДИН РАЗ замерили время и расстояние и УСРЕДНИВ нашли среднюю быстроту движения, то есть скорость.
ВТОРОЙ РАЗ замерили время и расстояние, причём и время и расстояние измеряли в другом месте. А затем УСРЕДНИЛИ и СРАВНИЛИ  второй раз.

А как же иначе?

Ещё раз. Пока мы не делили на количество временных раз, то есть не "усредняли по времени" мы не могли определить ни скорости, ни ускорения.

Значит по сути любое время - это прежде всего усреднение. Более того! Очень важно с каким типом точности времени мы имеем дело при измерении, то есть от того насколько часто мы производим измерение, или говоря по-другому с какой частотой.

Каждый следующий раз замеряя время, мы можем произвести СРАВНЕНИЕ с предыдущим показателем.

За один раз - находим точку отсчёта пространства-времени. За два раза усредняя и сравнивая находим скорость. За три раза находим меняется ли скорость и если меняется то увеличивается или уменьшается. Если в первый раз, при этом, мы сравнивали и усредняли координаты. То во второй раз процесс усреднения проходил дважды, то есть мы могли сравнивать уже скорости. Усреднение и сравнение. Ещё одно измерение координаты и времени даст возможность протестировать характер движения не просто на наличие ускорения, а на его равномерность. 

Это напоминает АЦП. Существует тактовая частота - точность измерения во времени. И битность - точность измерения интересующей величины. А количество раз измерения, усреднения и сравнения определяет глубину неравномерности в изменении измеряемой величины, выявляемую при этом.

Значит показатель степени при t говорит о потенциальном уровне нелинейности в изменении измеряемой величины. Или о том сколько раз было произведено СРАВНЕНИЕ.

Если на каком то из сравнений мы не получаем дополнительного изменения. то получается, что мы выбрали все "измерения времени" по которым изменяется данный процесс.

Вот в чём смысл воспринимаемых нами "измерений" у "времени". 

Итак есть поток времени, то есть просто разы повторяющегося цикла, определяемого операцией усреднения. И есть "измерения времени", понимаемые как степень нелинейности (или, если хотите, степень сложности) измеряемого процесса и определяемый операцией сравнения.

Как то так мне это сейчас видится...